Introduction to Break-Even Pricing

Image © Adobe Images

Understanding the concept of break-even pricing is a critical tool for businesses and financial market traders alike.

Traders must understand break-even analysis in order to maintain a winning strategy and businesses require the skill to make informed judgments regarding a product's short- and long-term profitability.

So, what is the break-even price?

It is the price at which all costs are covered at a given level of output.

There is no profit or loss at the break-even point.

A corporation may decide to price its goods below the break-even threshold, but we'll go through the many pricing techniques that may favour this choice later in the module.

Understanding the Breakeven Point

Let's start with a very basic breakeven calculation and work our way up from there.

Consider holding a bake sale and selling cookies in the student union as a social event for students. You don't want to lose money on the cookies, but you're not looking to turn a profit or
even pay your expenses.

You go grocery shopping for £24 and prepare 4 dozen cookies. (48 cookies). What is your cookie break-even point?

It is the entire cost divided by the number of cookies you plan to sell, as expressed by the following formula:

Break-Even Price = Costs / Number of Units

So, £24 divided by 48 is £.50, or 50 pence a cookie. What happens if you only sell 40 cookies?

£24 / 40 = £.60 would be the maths. If you sell fewer cookies, your break-even price rises.

One difficulty in determining break-even is that all of the factors are subject to change, and some are unknown. For example, it may be hard to predict precisely how much you will sell.

As a result, businesses often compute the break-even amount rather than the break-even price.

Focusing on quantity allows the business owner to answer the question, "How many products must I sell to break even given this set of costs and this price?"

The following formula calculates the break-even point:

Costs / Price = Break-Even Quantity (in Units)

In our cookie example, you know your cost after you've spent £24 on groceries.

What if you're going to sell the cookies for £1 each?

The calculation above states that units equal cost / price, thus in our situation, units = £24 / £1, or 24 cookies.

Trading Options and Break-even Pricing

When trading options on financial markets there will be a call option with a strike price of £100 and a premium paid of £2.50, the break-even price that the stock would have to get to is £102.50; anything above that level would be pure profit, anything below would imply a net loss.

Of course, this is a simplified example, but it illustrates why breakeven is important and how to calculate it.

Fixed and variable costs are included

Let's add another complexity to our example to make it more realistic and intriguing.

Your cookies have proven to be so popular that you decide to expand your distribution.

In actuality, you rent a professional kitchen and employ Helen, an expert baker, to handle the baking.

Your break-even point has now risen substantially. You must now pay the price of your kitchen as well as the staff.

For the sake of this exercise, imagine Helen works 20 hours per week and that you pay her £20 per hour, including all taxes and benefits.

The kitchen is rented for £100 a week, which includes all equipment and utilities.

Those are fixed expenses that will not alter regardless of how many cookies you sell. Even if you didn't bake anything, you'd still have to pay £100 in rent and £400 in salary each week.

These are your fixed expenses.

Fixed costs do not alter when output levels rise or fall. Your weekly fixed expenses are £500.

You must now purchase the ingredients for the cookies. When you sum up the ingredient expenditures for a single big batch of cookies, you get £7.20 for a batch of 12 dozen (144) cookies.

When you divide it by 144 cookies, you'll see that each cookie costs £.05 in food prices (£7.20 / 144 cookies = £.05).

In other words, each cookie you sell has a variable cost of £.05.

Variable expenses alter when output increases or decreases.

Including these many forms of expenses complicates the break-even calculation, as demonstrated below:

Vn + FC = pn
p = cost

The answer is yes.

V = variable unit cost
FC stands for fixed costs.

We may use this equation to get either the break-even price or the break-even quantity.

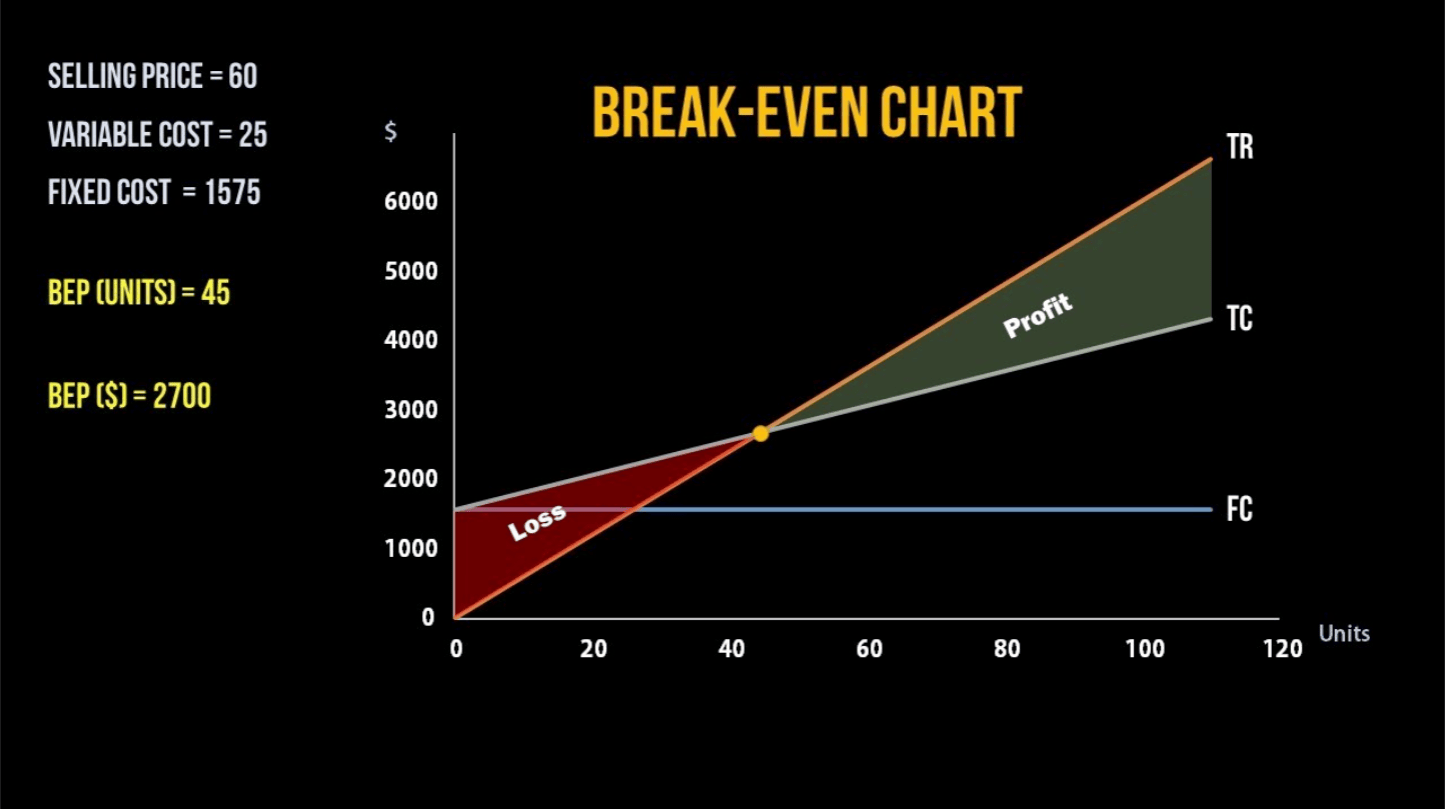
Calculating the Break-Even Point

You can probably only make a specific quantity of cookies each week—say, 2,500 cookies—so you can determine the break-even price based on that knowledge.

The formula for doing so is as follows:

(Vn + FC) / n = p
n = 2,500
V = £.05

FC = £500
As a result, p = ((£.05 x 2,500) + £500) / 2,500
p = (£125 + £500) / 2,500
p = £.25

Your cookie break-even point is 25 pence.

That doesn't imply it's the proper market price for the cookies, nor does it indicate you'll be able to sell 2,500 cookies at whatever price you choose.

It merely informs you of the price and amount at which you will meet all of your expenditures.

Break-Even Quantity Calculation

Assume you've decided on pricing and need to calculate your break-even point.

You are an excellent marketing student, so you have spoken with the individuals who are likely to purchase your cookies or anything else and you know what pricing is a steal and what price is too much.

You compared the pricing to that of competitors. And you've weighed the cost of your cookie against the cost of doughnuts and ice cream (both of which are 'substitutes' for your product).

All of your research has led you to a pricing of £2 per cookie, but you want to ensure that your firm does not lose money: You must compute the break-even point.

The formula for doing so is as follows:

n = FC /( p – V)

Using the same variables as inputs, your equation reads like this: n = £500 / (£2 – £.05)
n = £500 / £1.95
for a total of 256.41 cookies

So, let's round up to 257 cookies as the break-even amount. Does this imply you retain the whole £2 profit for every cookie after 257?

Unfortunately, no.

To begin, you must pay the variable cost of each cookie (£.05 each cookie), which means you only earn £1.95 every cookie sold (until you've crossed the break-even mark).

Second, our basic break-even analysis did not account for all expenses. After you've determined the product expenses and price, you'll need to spend in cookie advertising and distribution.

You'll also want to include in your time (i.e., pay yourself) and profit into the overall fixed expenses.

For example, if you wanted to make £600 per week, you would need to add it to the £500 fixed expenses for the kitchen and Helen.

Breakthrough in Business Strategy

It's a bit simpler to think about price goals now that we have a cost example. If you decide to price your cookies profitably, you just add a profit (£1 a cookie, say) to the break-even price.

That approach, however, ignores the client entirely since a profit orientation is solely concerned with the company.

What if you discovered that your campus shops and vending machines offer a major cookie chain for 75 pence?

You may opt to match that price and compete on that basis if you use a competitor-oriented pricing strategy.

The disadvantage of this method is that it ignores the importance your consumers place on a fresh, local product—in this case, your cookies—made from high-quality ingredients.

A customer-oriented pricing method enables you to use break-even statistics as one input to your price, but it also incorporates your customers' views and the overall worth of your product
into the pricing review.